On Score / Clock Management
- Hamilton runs up the middle with Don Jackson on 1st down for 5 yards. 8 seconds come off the clock, and Hamilton snaps it with 17 on the play clock for their 2nd down play.
- On second down, Hamilton runs again with Don Jackson for 0 yards.
For third down, at the time of snap, there are 27 seconds left. The game clock is running at this point (I believe TSN just didn't start the play clock). At this point, especially, Hamilton should be using all of the clock. - The clock has not stopped for this entire series of downs, and Hamilton somehow have only killed 21 seconds, despite running two running plays. Of course, Tim White catches a TD, and the clock stops with 19 seconds left.
Then..
The Situation:
In today's Hamilton vs. Ottawa game there were a couple of interesting choices in the final moments of the game. Firstly, Hamilton played the sequence before the touchdown very weirdly. Tim White was pushed out of bounds at Ottawa's 8 yard line with 47 seconds left. At this point, Ottawa does still have their timeout left.
Obviously, if you're Hamilton you need to score, but in the back of your mind you should be trying to kill as much time as possible so that Ottawa cannot win or tie (we'll get to that) if they get the ball back.
Obviously, if you're Hamilton you need to score, but in the back of your mind you should be trying to kill as much time as possible so that Ottawa cannot win or tie (we'll get to that) if they get the ball back.
So, 47 seconds left, ball on Ottawa's 8 yard line:



For whatever reason, everyone is celebrating, etc, and out trots the kicking unit???? At this point it's a 1 point lead for Hamilton with 19 seconds left. They end up making the extra point to up by 2. Great.
My win probability model did not like the choice to kick the XP, giving the 2 pt attempt about a +2.5% gain in win probability if they went for two, regardless of if they actually were successful or not. Marshall Ferguson called it best when he said that the "1 point convert doesn't really get you anything."
Let's walkthrough possible scenarios to see how that 2.5% lines up. We can assume Ottawa's motivation is constant whether down 1, 2, or 3.
Obviously, a kick return TD basically wins the game for Ottawa and should have no impact on our (Hamilton's) convert choice.
We're going to make some very imperfect assumptions here, but it's really just to validate the above 2.5%. Both scenarios will have the same assumptions, so it should be a pretty fair comparison.
Let's say Ottawa has a 15% chance to move the ball into FG range, and they're going to make that FG ~65% of the time. We also will give them a 5% rouge chance. If the game goes to overtime, we will assume a coin flip (50%). We can also assume that Hamilton has a 56% chance of making a 2-pt convert, and a 94% chance of making a 1-pt convert.
My win probability model did not like the choice to kick the XP, giving the 2 pt attempt about a +2.5% gain in win probability if they went for two, regardless of if they actually were successful or not. Marshall Ferguson called it best when he said that the "1 point convert doesn't really get you anything."
Let's walkthrough possible scenarios to see how that 2.5% lines up. We can assume Ottawa's motivation is constant whether down 1, 2, or 3.
Obviously, a kick return TD basically wins the game for Ottawa and should have no impact on our (Hamilton's) convert choice.
We're going to make some very imperfect assumptions here, but it's really just to validate the above 2.5%. Both scenarios will have the same assumptions, so it should be a pretty fair comparison.
Let's say Ottawa has a 15% chance to move the ball into FG range, and they're going to make that FG ~65% of the time. We also will give them a 5% rouge chance. If the game goes to overtime, we will assume a coin flip (50%). We can also assume that Hamilton has a 56% chance of making a 2-pt convert, and a 94% chance of making a 1-pt convert.
Hamilton 2pt:
Ottawa: 56% (Hamilton made 2-pt conversion) * 15% (drive into FG range) * 65% (make FG) * 50% (WP in OT) = 2.7% chance of Ottawa winning.
Ottawa: 44% (Hamilton missed 2pt conversion) * 15% (drive into FG range) * 65% (make FG) * 100% (Ottawa wins the game) = 4.29% chance of Ottawa winning
Ottawa: 44% (Hamiton missed 2pt conversion) * 15% (drive into FG range) * 5% (rouge chance) * 50% (WP in OT) = extremely LOW. negligible.
Ottawa: 44% (Hamilton missed 2pt conversion) * 15% (drive into FG range) * 65% (make FG) * 100% (Ottawa wins the game) = 4.29% chance of Ottawa winning
Ottawa: 44% (Hamiton missed 2pt conversion) * 15% (drive into FG range) * 5% (rouge chance) * 50% (WP in OT) = extremely LOW. negligible.
1pt:
Ottawa: 94% (Ham made 1pt convert) * 15% (drive into FG range) * 65% (make FG) * 100% (Ottawa wins the game) = 9.1% chance of winning for Ottawa
Ottawa: 6% (Ham missed 1pt convert) * 15% (drive into FG range) * 5% (rouge chance) * 50% (game goes to OT) = extremely LOW. negligible.
Ottawa: 6% (Ham missed 1pt convert) * 15% (drive into FG range) * 5% (rouge chance) * 50% (game goes to OT) = extremely LOW. negligible.
Conclusion
If you compare these, going for 2 gives Ottawa a combined ~7% chance of winning, regardless of if you make it or not. Conversely, going for 1 gives Ottawa a ~9% chance of winning. It is very clear that going for 2 is the correct choice for Hamilton.
It is also worth noting that if Hamilton just manages the clock correctly, this choice basically does not matter.
It is also worth noting that if Hamilton just manages the clock correctly, this choice basically does not matter.
I also think Ottawa made a 2pt-conversion mistake. My win probability model also disagreed with Ottawa's choice in the 3rd quarter to kick an extra point after they pulled to within 2. Again, this was a small mistake, with the WP change like 2-3%, but it is such a simple fix.
In general for converts, it seems like you should take any chance you can to tie the game up.
In general for converts, it seems like you should take any chance you can to tie the game up.
CLOCK
This has driven me crazy all year, but there's a fantastic example of it in this game. The refs just don't start the play clock. With 3 minutes left in the 3rd quarter, RJ Harris made a catch to turn it into a 3rd and 2. At this point, the clock is generously at 3:02.

The ball is spotted, Ottawa initially sends out a heavy set to go for it, but then reconsiders and sends out the punt unit. All the while, the play clock still has not been blown in.

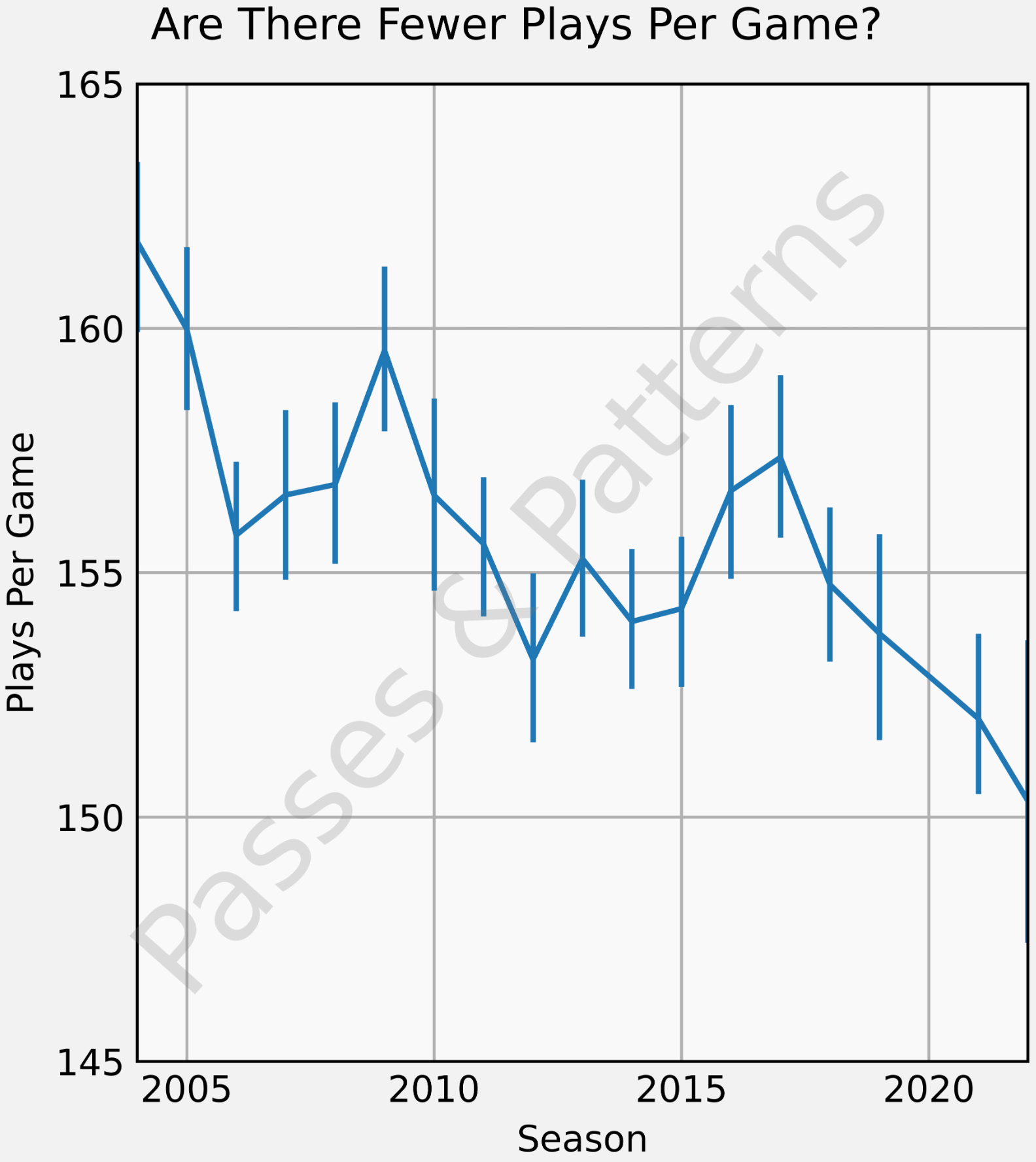
The 20 second play clock finally starts, 40 seconds after Harris made the catch. One of the single easiest ways to increase scoring is going to be to blow the plays in earlier. As a fan, we get to see more and more action. Chris Clement had a great thread about scoring in the CFL this year, linked here, where he also shows this graphic in plays per game, likely attributed to "neither coaches nor officials nor the league pushing teams to get their asses in gear."